Binomial Queue

Binomial Queue is a #Priority Queue/Heap that seeks to improve Leftist Heap’s and Skew Heap’s Insert. Unlike those, it is a collection of Linked List Tree.

Illustration

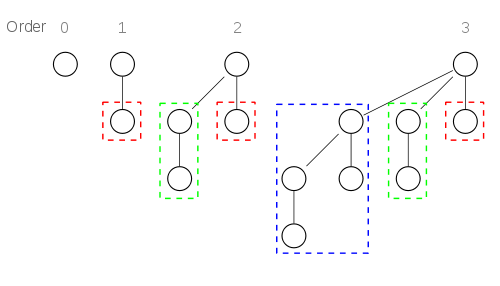
Analysis

Insert will result in \(O(1)\).
Merge and DeleteMin will result in \(O(\log N)\).
FindMin could result in \(O(\log N)\) if the minimum is not known

Implementation

#ifndef _BinomialQueue_H

struct BinNode;
struct Collection;
typedef struct BinNode *Position;
typedef struct Collection *BinQueue;

BinQueue Initialise(void);
int IsEmpty(BinQueue H);
ElementType FindMin(BinQueue H);
BinTree CombineTrees(BinTree T1, BinTree T2);
BinQueue Merge(BinQueue H1, BinQueue H2);
ElementType DeleteMin(BinQueue H);

#endif

struct BinNode {
  ElementType Element;
  Position    LeftChild;
  Position    NextSibling;
};

/**
 *  Return the result of merging equal-sized T1 and T2
 */
BinTree CombineTrees(BinTree T1, BinTree T2) {
  if (T1->Element > T2->Element)
    return CombineTrees(T2, T1);
  T2->NextSibling = T1->LeftChild;
  T1->LeftChild = T2;
  return T1;
}

/**
 *  Merge two binomial queues
 *  Not optimised for early termination
 *  H1 contains merged result
 */
BinQueue Merge(BinQueue H1, BinQueue H2) {
  BinTree T1, T2, Carry = NULL;

  if (H1->CurrentSize + H2->CurrentSize > Capacity)
    Error("Merge would exceed capacity");

  H1->CurrentSize += H2->CurrentSize;
  for (int i = 0, j = 1; j <= H1->CurrentSize; i++, j *= 2) {
    T1 = H1->TheTrees[i];
    T2 = H2->TheTrees[i];

    switch (!!T1 + 2*!!T2 + 4*!!Carry) {
      case 0: // No trees
      case 1: // Only H1
        break;
      case 2: // Only H2
        H1->TheTrees[i] = T2;
        H2->TheTrees[i] = NULL;
        break;
      case 4: // Only Carry
        H1->TheTrees[i] = Carry;
        Carry = NULL;
        break;
      case 3: // H1 and H2
        Carry = CombineTrees(T1, T2);
        H1->TheTrees[i] = H2->TheTrees[i] = NULL;
        break;
      case 5: // H1 and Carry
        Carry = CombineTrees(T1, Carry);
        H1->TheTrees[i] = NULL;
        break;
      case 6: // H2 and Carry
        Carry = CombineTrees(T2, Carry);
        H2->TheTrees[i] = NULL;
        break;
      case 7: // All Trees
        H1->TheTrees[i] = Carry;
        Carry = CombineTrees(T1, T2);
        H2->TheTrees[i] = NULL:
        break;
    }
  }

  return H1;
}

ElementType DeleteMin(BinQueue H) {
  int MinTree;    // The tree with the minimum item
  BinQueue DeletedQueue;
  Position DeletedTree, OldRoot;
  ElementType MinItem;

  if (IsEmpty(H)) {
    Error("Empty binomial queue");
    return -Infinity;
  }

  MinItem = Infinity;
  for (int i = 0; i < MaxTrees; i++) {
    if (H->TheTrees[i] && H->TheTrees[i]->Element < MinItem) {
      // Update minimum
      MinItem = H->TheTrees[i]->Element;
      MinTree = i;
    }
  }

  DeletedTree = H->TheTrees[MinTree];
  OldRoot = DeletedTree;
  DeletedTree = DeletedTree->LeftChild;
  free(OldRoot);

  DeletedQueue = Initialise();
  DeletedQueue->CurrentSize = (1 << MinTree) - 1;
  for (int j = MinTree - 1; j >= 0; j--) {
    DeletedQueue->TheTrees[j] = DeletedTree;
    DeletedTree = DeletedTree->NextSibling;
    DeletedQueue->TheTrees[j]->NextSibling = NULL;
  }

  H->TheTrees[MinTree] = NULL;
  H->CurrentSize -= DeletedQueue->CurrentSize + 1;

  Merge(H, DeletedQueue);
  return MinItem;
}