Relation is a #202204281446 of #202204281552 \((a, b)\) where \(a \in A\) and \(b \in B\) assuming that \(A\) and \(B\) are sets, which \(a\) is related to \(b\), denoted \(a R b\). In this sense, \(A\) is the domain of this relation and \(B\) is the co-domain. We could say that it is a relation from A to B.
Let \(A = \{0, 1, 2\}\) and \(B = \{1, 2, 3\}\), and let’s say that element \(a\) in \(A\) is related to element \(b\) in \(B\) if and only if \(a < b\). This relation could be expressed in a set as \(\{(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)\}\). The result of \(A \times B\) is \(\{(0, 1), (0, 2), (0, 3), (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3)\}\). It is not hard to see that it is a 202204281535 of 202204281601# of \(A\) and \(B\) aka \(A \times B\).
An arrow diagram could be drawn from a relation. The following diagram shows the relation from \(X\) to \(Y\):
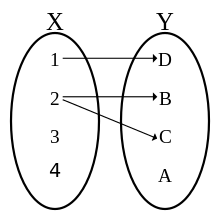
Note: The arrows are coming from domain to co-domain which illustrate that \(x\) in \(X\) is related to \(y\) in \(Y\).
Relation could be a 202204282055# if it met the criteria.