Parity Polynomial \(b(D)\) is defined as below using several facts from #Cyclic Code and #Generator Polynomial:
$$ \begin{align} x(D) &= b(D) + D^{n-k} m(D)\\ x(D) &= a(D) g(D)\\ a(D) g(D) &= b(D) + D^{n-k} m(D)\\ a(D) &= b(D) / g(D) + D^{n-k} m(D) / g(D)\\ D^{n-k} m(D) / g(D) &= a(D) - b(D) / g(D) (\mod 2)\\ D^{n-k} m(D) / g(D) &= a(D) + b(D) / g(D)\\ b(D) &= D^{n-k} m(D) \mod g(D) \end{align} $$
Modulus \(g(D)\) is done by eliminating similar Ds until we reach the lowest exponentiation using long division. Use the highest possible degree polynomial to divide \(g(D)\) using \(D^{n-k} m(D)\). The long division shown below illustrates how to do it:
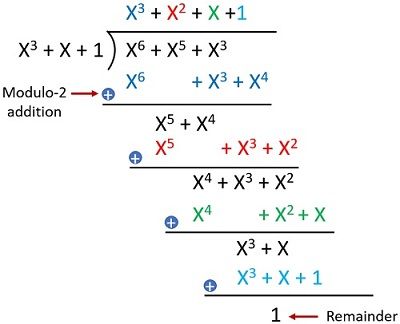
Where:
- \(X^3 + X + 1 = g(X)\)
- \(X^6 + X^5 + X^3 = X^{n-k} m(X)\)